I. Introduction▲
Nous avons vu dans le tutoriel précédent comment calculer l'éclairage par pixel. Pour cela, nous avons besoin d'une normal map qui représente les normales de la surface. Nous avons aussi besoin de calculer un espace local par vertex qui nous permet de calculer le vecteur vers la lumière qui nous sert pour le calcul du DOT3 bump mapping. Comme nous l'avons vu, bien qu'il soit assez peu visible dans le tutoriel précédent, le fait d'utiliser les vertex pour envoyer le vecteur vers la lumière pose problème. En effet, l'interpolation des vecteurs donne un résultat non normalisé, et on risque aussi d'avoir des artefacts plutôt gênants qui éclairent le polygone d'une façon incohérente par rapport à la position de la lumière. Pour résoudre ce problème, nous avons besoin d'un mécanisme qui nous permet d'avoir des vecteurs qui pointent tous effectivement dans la direction de la lumière, pas seulement au niveau des vertex, mais partout sur le polygone. En plus, il serait intéressant de pouvoir améliorer par la même occasion le problème de normalisation des vecteurs pour avoir un éclairage plus cohérent. Pour cela, je vais présenter une solution basée sur l'utilisation d'une cube map particulière appelée cube map de normalisation.
Un autre problème du tutoriel précédent est que nous ne pouvons plus afficher de lumières colorées. En effet, l'extension env_dot3 utilise la couleur des vertex pour effectuer le calcul de DOT3 bump mapping. Comme nous n'avons pas de moyen standard pour pouvoir modifier la couleur de sortie du multitexturing sans utiliser de fragment program/shader, je vais présenter une solution basée sur un rendu multipasse.
II. La « cube map » de normalisation▲
Nous allons voir dans cette partie ce qu'est une cube map de normalisation, pourquoi et comment l'utiliser.
II-A. Pourquoi avons-nous besoin d'une cube map de normalisation▲
Comme je l'ai dit dans l'introduction, l'utilisation de la couleur des vertex pour envoyer un vecteur n'est pas satisfaisante. Il nous faut un mécanisme permettant d'avoir des vecteurs qui pointent bien tous vers la lumière, et, si possible, qui soient normalisés. Comme pour le light mapping, la solution aux problèmes d'interpolation se base sur l'utilisation de textures. Néanmoins, contrairement au light mapping, ici, nous n'utiliserons pas une texture 2D ou 3D, mais une cube map. L'avantage de la cube map est qu'elle permet de calculer automatiquement une projection multidirectionnelle de textures. Si vous ne voyez pas ce qu'est une projection multidirectionnelle de texture, imaginez simplement une projection de texture dans une direction, puis effectuez cette même projection dans les six directions d'un cube. Voilà, vous y êtes, la cube map permet de projeter six textures comme si elles étaient sur un cube projeté à l'infini. À l'origine, les cube maps étaient prévues pour calculer des pseudo-réflexions sur des objets, mais en les utilisant d'une certaine manière, elles peuvent résoudre nos problèmes de vecteurs vers la lumière. C'est ce que nous allons voir tout de suite.
II-B. Qu'est-ce qu'une cube map de normalisation▲
Comme nous l'avons vu au-dessus, on peut appréhender les cube maps comme des cubes infiniment lointains autour d'une position. Ceci permet d'avoir à moindre coût une projection dans les six directions d'un cube. Tout ceci est bien beau, mais en quoi cela va-t-il résoudre notre problème de vecteurs ? Tout simplement en remplissant notre cube map de vecteurs.
En fait, ce qu'on appelle une cube map de normalisation n'est rien d'autre qu'une cube map dont chaque texel est un vecteur pointant vers le centre de la cube map. Ainsi, lorsqu'on projette notre cube map sur un polygone, on obtient un polygone dont tous les pixels sont des vecteurs dirigés vers le centre de la cube map. Il ne nous reste donc plus qu'à placer notre cube map à l'emplacement de la lumière pour que notre polygone soit couvert de vecteurs vers la lumière. En plus, comme chaque texel de la cube map est un vecteur normalisé, le problème des vecteurs non normalisés à cause de l'interpolation entre les vertex est réduit. Par contre, il n'est pas non plus totalement éliminé, étant donné qu'on peut toujours avoir de l'interpolation entre les texels de la cube map. Néanmoins, le résultat est très nettement supérieur à celui de la méthode par vertex.
Comme souvent, un schéma explique mieux qu'un long discours.
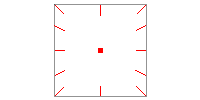
Voici le contenu d'une cube map de normalisation : chaque texel représente un vecteur pointant vers le centre de la cube map.
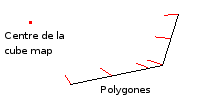
Et voilà le résultat de l'utilisation d'une cube map sur des polygones : les côtés de la cube map sont projetés sur les polygones, les remplissant de vecteurs dirigés vers le centre de la cube map.
Maintenant que nous savons ce qu'est une cube map de normalisation, nous allons voir comment la calculer.
II-C. Comment calculer la cube map de normalisation▲
Tout d'abord, nous allons nous occuper de gérer l'extension. Comme pour l'extension env_dot3, les cube maps n'ont pas besoin d'utiliser de nouvelles fonctions. Le chargement de l'extension est donc simple, il suffit de vérifier si la carte supporte les cube maps. La fonction de chargement des extensions devient donc ça :
void initExtensions()
{
if (glutExtensionSupported("GL_ARB_multitexture"))
{
glMultiTexCoord2fARB = (PFNGLMULTITEXCOORD2FARBPROC)wglGetProcAddress("glMultiTexCoord2fARB");
glMultiTexCoord3fARB = (PFNGLMULTITEXCOORD3FARBPROC)wglGetProcAddress("glMultiTexCoord3fARB");
glMultiTexCoord4fARB = (PFNGLMULTITEXCOORD4FARBPROC)wglGetProcAddress("glMultiTexCoord4fARB");
glActiveTextureARB = (PFNGLACTIVETEXTUREARBPROC)wglGetProcAddress("glActiveTextureARB");
glClientActiveTextureARB = (PFNGLCLIENTACTIVETEXTUREARBPROC)wglGetProcAddress("glClientActiveTextureARB");
if (!glActiveTextureARB || !glMultiTexCoord2fARB || !glMultiTexCoord3fARB
|| !glMultiTexCoord4fARB || !glClientActiveTextureARB)
{
fprintf(stderr,"impossible d'initialiser l'extension GL_ARB_multitexture\n");
exit(0);
}
}
else
{
fprintf(stderr,"votre carte ne supporte pas l'extension GL_ARB_multitexture\n");
exit(0);
}
if (glutExtensionSupported("GL_EXT_texture3D"))
{
glTexImage3DEXT = (PFNGLTEXIMAGE3DEXTPROC) wglGetProcAddress("glTexImage3DEXT");
glTexSubImage3DEXT = (PFNGLTEXSUBIMAGE3DEXTPROC) wglGetProcAddress("glTexSubImage3DEXT");
if (!glTexImage3DEXT || !glTexSubImage3DEXT)
{
fprintf(stderr,"impossible d'initialiser l'extension GL_EXT_texture3D\n");
exit(0);
}
}
else
{
fprintf(stderr,"votre carte ne supporte pas l'extension GL_ARB_multitexture\n");
exit(0);
}
if (!glutExtensionSupported("GL_ARB_texture_env_dot3"))
{
fprintf(stderr,"votre carte ne supporte pas l'extension GL_ARB_texture_env_dot3\n");
exit(0);
}
if (!glutExtensionSupported("GL_ARB_texture_cube_map"))
{
fprintf(stderr,"votre carte ne supporte pas l'extension GL_ARB_texture_cube_map\n");
exit(0);
}
}Maintenant, nous pouvons voir comment calculer la cube map. Pour cela, j'utilise deux fonctions. La première, getCubeVector, permet de récupérer un vecteur pointant vers le centre de la cube map en fonction de la face du cube et de la position du texel dans la face. Cette fonction est assez simple à comprendre et donne le code suivant :
void getCubeVector(int i, int cubesize, int x, int y, float *vector)
{
float s, t, sc, tc, mag;
s = ((float)x + 0.5) / (float)cubesize;
t = ((float)y + 0.5) / (float)cubesize;
sc = s*2.0 - 1.0;
tc = t*2.0 - 1.0;
// selon la face passée en paramètre, on calcule le vecteur vers le centre de la cube map.
switch (i)
{
case 0:
vector[0] = 1.0;
vector[1] = -tc;
vector[2] = -sc;
break;
case 1:
vector[0] = -1.0;
vector[1] = -tc;
vector[2] = sc;
break;
case 2:
vector[0] = sc;
vector[1] = 1.0;
vector[2] = tc;
break;
case 3:
vector[0] = sc;
vector[1] = -1.0;
vector[2] = -tc;
break;
case 4:
vector[0] = sc;
vector[1] = -tc;
vector[2] = 1.0;
break;
case 5:
vector[0] = -sc;
vector[1] = -tc;
vector[2] = -1.0;
break;
}
// on normalise le vecteur.
mag = 1.0/sqrt(vector[0]*vector[0] + vector[1]*vector[1] + vector[2]*vector[2]);
vector[0] *= mag;
vector[1] *= mag;
vector[2] *= mag;
}La deuxième fonction utilisée est celle qui calcule effectivement la cube map et l'envoie à OpenGL. Cette fonction prend en paramètre la taille en texels d'un côté de la cube map et génère donc une cube map de normalisation. Pour cela, elle utilise un buffer de la taille d'un côté de la cube map et s'en sert pour générer les six côtés différents en utilisant la fonction getCubeVector pour récupérer chaque texel. Le code de la fonction donne donc ça :
void generateNormalisationCubeMap(int size)
{
glEnable(GL_TEXTURE_CUBE_MAP_ARB);
//génère l'objet de texture OpenGL en mémoire vidéo
glGenTextures(1,&normalCubeMapId);
glBindTexture(GL_TEXTURE_CUBE_MAP_ARB, normalCubeMapId);
float vector[3];
int i, x, y;
GLubyte *pixels = new GLubyte[size*size*3];
// on configure la texture. On utilise un filtrage linéaire pour ne pas avoir à
// générer les mipmaps.
glTexParameteri(GL_TEXTURE_CUBE_MAP_ARB, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP_ARB, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP_ARB,GL_TEXTURE_MAG_FILTER,GL_LINEAR);
glTexParameteri(GL_TEXTURE_CUBE_MAP_ARB,GL_TEXTURE_MIN_FILTER,GL_LINEAR);
// Pour chaque face
for (i = 0; i < 6; i++)
{
// on remplit le buffer de texture avec des vecteurs
for (y = 0; y < size; y++)
{
for (x = 0; x < size; x++)
{
getCubeVector(i, size, x, y, vector);
pixels[3*(y*size+x) + 0] = 128 - 127*vector[0];
pixels[3*(y*size+x) + 1] = 128 - 127*vector[1];
pixels[3*(y*size+x) + 2] = 128 - 127*vector[2];
}
}
// on envoie le buffer de texture à OpenGL
gluBuild2DMipmaps(GL_TEXTURE_CUBE_MAP_POSITIVE_X_ARB+i,GL_RGB8,size,size,GL_RGB,GL_UNSIGNED_BYTE,pixels);
}
delete [] pixels;
glDisable(GL_TEXTURE_CUBE_MAP_ARB);
}Ici, je n'utilise qu'un filtrage linéaire, je n'ai donc pas généré les différents niveaux de mipmap, mais il faudrait les générer en cas d'utilisation de filtrage autre.
Ces fonctions sont des versions légèrement modifiées des fonctions utilisées dans les démos de nVidia sur le bump mapping qu'on peut trouver dans la section développeurs du site nvidia.com.
III. Modification du rendu▲
Maintenant que nous savons comment calculer notre cube map de normalisation, nous allons voir comment l'utiliser. Ensuite, nous verrons comment faire pour avoir des lumières colorées, puis nous verrons le rendu final comme sur tous les tutoriels précédents.
III-A. Utiliser la cube map de normalisation▲
Maintenant que nous avons notre cube map de normalisation, il faut encore savoir comment l'utiliser. En fait, c'est très simple. Pour cela, il suffit de calculer pour chaque vertex les bonnes coordonnées de texture pour la cube map, et la projection automatique de la cube map va se charger pour nous de recouvrir le polygone comme il faut.
Ces coordonnées de textures sont en fait très simple à calculer, il s'agit tout simplement… d'un vecteur encore une fois. En effet, notre cube map peut être vu comme une sorte particulière de texture en 3D, donc pour récupérer ses informations, il faut lui passer des coordonnées de texture 3D. Voici un petit schéma qui montre comment se calculent les coordonnées de texture de la cube map.
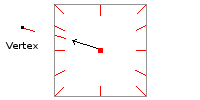
Ici, le vecteur noir représente des coordonnées de texture qui vont adresser une face de la cube map, ensuite, la carte graphique va se charger de tous les calculs de projection. On peut noter ici que contrairement au tutoriel précédent, le vecteur calculé est le vecteur de la lumière vers le vertex. Dans le tutoriel précédent, nous avions fait l'inverse. Le problème est que, pour calculer notre bump mapping, nous avons besoin d'un vecteur allant du vertex vers la lumière, mais notre cube map contient des vecteurs dans le mauvais sens comme le montre le schéma suivant.
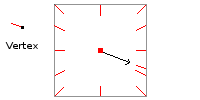
Nous voulons donc un vecteur dirigé dans l'autre sens comme sur le premier schéma, c'est pour ça que nous calculons le vecteur de la lumière vers le vertex.
À part ce point, et le fait que les unités de textures soient configurées de manières différentes du tutoriel précédent, le code de la méthode pour ajouter une lumière est relativement proche de celui du tutoriel précédent. J'ai néanmoins changé le nom de la méthode en addLightCubeMap pour bien faire la différence entre les deux tutoriels. Le code de la méthode donne donc :
void Model::addLightCubeMap(Light& light)
{
Vecteur lightPos = light.getPosition();
glBegin(GL_TRIANGLES);
for(int i = 0;i < nbFaces; i++)
{
for (int j = 0; j < 3; j++)
{
int vertexIndex = faces[i].vertexIndex[j];
// on calcule le vecteur lumière->vertex projeté dans l'espace local du vertex
Vecteur tempVect = vertex[vertexIndex] - lightPos;
Vecteur lightToVertex;
lightToVertex.x = tangents[vertexIndex]*tempVect;
lightToVertex.y = binormals[vertexIndex]*tempVect;
lightToVertex.z = normals[vertexIndex]*tempVect;
// nous avons donc maintenant le vecteur de la lumière vers le vertex
// transforme dans l'espace local du vertex.
// on l'envoie en tant que coordonnées de texture pour la cube map
glMultiTexCoord3fARB(GL_TEXTURE0_ARB,lightToVertex.x,lightToVertex.y,lightToVertex.z);
// maintenant, on envoie les coordonnées de textures
// la seconde unité de texture contient la normal map, ce sont donc
// les mêmes coordonnées de textures que la scène
TexCoord &tc = texCoords[faces[i].texCoordIndex[j]];
glMultiTexCoord2fARB(GL_TEXTURE1_ARB,tc.u,tc.v);
// la troisième unité de texture contient la texture 3D d'atténuation,
// on calcule donc l'éclairage
Vecteur &v = vertex[vertexIndex];
Vecteur lightTexCoord = light.computeLighting(v);
glMultiTexCoord3fARB(GL_TEXTURE2_ARB,lightTexCoord.x,lightTexCoord.y,lightTexCoord.z);
// la quatrième unité de texture contient la texture de diffuse,
// donc les coordonnées de textures de la scène
glMultiTexCoord2fARB(GL_TEXTURE3_ARB,tc.u,tc.v);
glVertex3f(v.x,v.y,v.z);
}
}
glEnd();
}Comme d'habitude, la méthode suppose qu'OpenGL est bien configuré, à savoir : la première unité de texture contient la cube map de normalisation, la deuxième contient la normal map configurée pour effectuer la passe de DOT3, la troisième contient la texture 3D d'atténuation et la dernière contient la texture diffuse de la scène. De plus, le blending doit être positionné en mode additif pour que les lumières puissent bien être ajoutées à la scène.
III-B. Rendu des lumières colorées▲
Ça y est nous avons un rendu de l'éclairage par pixel correct, mais il nous manque quand même un élément important que nous avions avec l'éclairage par vertex et les light maps : nos lumières ne sont plus colorées. Le problème, c'est que nous ne pouvons plus modifier la couleur de notre lumière via glColor car le fait d'utiliser l'extension env_dot3 nous génère forcément un résultat en niveaux de gris, quelle que soit la couleur précédente du pixel. Comme il n'existe pas d'extension standard pour modifier la couleur après la passe de DOT3 (on peut le faire avec des extensions propriétaires comme les register combiner ou encore les textures shaders sur GeForce 4, mais je tiens à n'utiliser que des extensions validées par l'ARB), et comme on n'utilise pas de fragment program/shaders ici, il va falloir passer à un rendu multipasse pour obtenir nos lumières colorées.
Pour cela, il nous suffit d'effectuer une passe supplémentaire par lumière en multipliant le résultat précédent par la couleur souhaitée. Pour éviter au maximum les changements d'état OpenGL, on peut organiser ça en rendant d'abord toutes les lumières avec le bump mapping, puis on effectue une seconde passe en multipliant toutes les lumières par leur couleur. Le problème, c'est que si on utilise le blending multiplicatif simple, on ne pourra effectuer cette méthode qu'avec une seule lumière. En effet, le fait de multiplier la scène va rendre noires toutes les parties qui ne sont pas dans la lumière courante, on obtient donc seulement l'intersection de toutes les lumières de la scène. Il nous faut donc trouver une autre solution.
Cette solution est toute simple, elle consiste à utiliser le blending multiplicatif+additif présenté dans le premier tutoriel sur le light mapping. Ainsi, on peut multiplier la lumière par sa couleur sans pour autant noircir le reste de la scène. Cela donne un rendu de la scène plus clair et les lumières peuvent saturer vers le blanc, mais le résultat est acceptable.
L'algorithme de rendu donne donc le pseudo-code suivant :
Rendu de la couleur ambiante
Blending additif
Pour chaque lumière :
Ajouter la passe de bump mapping à la scène
Fin pour
Blending multiplicatif+additif
Pour chaque lumière :
Multiplier la scène précédente par la couleur de la lumière.
Fin pourComme vous pouvez le voir, il nous faut pouvoir afficher juste la couleur de nos lumières pour la deuxième passe. Ceci correspond en fait à une passe d'affichage de la texture d'atténuation, autrement dit : une simple passe de light mapping comme nous l'avons fait dans les tutoriels 2 et 3, mais sans multiplier le tout par la texture diffuse de la scène. Ici, nous ne rendons que la light map dynamique avec la couleur de la lumière. Ceci nous donne donc la méthode suivante :
void Model::renderColor(Light& light)
{
glColor3f(light.getColor().r,light.getColor().g,light.getColor().b);
Vecteur lightPos = light.getPosition();
glBegin(GL_TRIANGLES);
for(int i = 0;i < nbFaces; i++)
{
for (int j = 0; j < 3; j++)
{
Vecteur &v = vertex[faces[i].vertexIndex[j]];
Vecteur lightTexCoord = light.computeLighting(v);
// la première unité de texture contient la texture d'atténuation
glMultiTexCoord3fARB(GL_TEXTURE0_ARB,lightTexCoord.x,lightTexCoord.y,lightTexCoord.y);
glVertex3f(v.x,v.y,v.z);
}
}
glEnd();
}III-C. Le rendu final▲
Maintenant que nous avons tous les éléments en main pour rendre nos lumières, nous pouvons voir comment effectuer le rendu final. Voici d'abord le code nécessaire pour rendre les lumières par pixel correctement sans prendre en compte la couleur des lumières :
// on configure la première unité de texture : elle contient la texture de la scène
glActiveTextureARB(GL_TEXTURE0_ARB);
glEnable(GL_TEXTURE_2D);
glBindTexture(GL_TEXTURE_2D, textureId);
glTexEnvf(GL_TEXTURE_ENV,GL_TEXTURE_ENV_MODE,GL_MODULATE);
// on effectue le rendu de la lumière ambiante
model->initLighting(ambiant);
if (drawLocalSpace)
{
glDisable(GL_TEXTURE_2D);
model->drawLocalSpace();
}
// on doit reconfigurer les unités de textures
// la première unité contient la cube map de normalisation
glActiveTextureARB(GL_TEXTURE0_ARB);
glEnable(GL_TEXTURE_CUBE_MAP_ARB);
glBindTexture(GL_TEXTURE_CUBE_MAP_ARB, normalCubeMapId);
// on souhaite que la cube map remplace la couleur des vertex
glTexEnvf(GL_TEXTURE_ENV,GL_TEXTURE_ENV_MODE,GL_REPLACE);
// la deuxième unité de texture contient la normal map
glActiveTextureARB(GL_TEXTURE1_ARB);
glEnable(GL_TEXTURE_2D);
glBindTexture(GL_TEXTURE_2D, normalMapId);
// on configure la normal map pour qu'elle effectue la passe de DOT3
glTexEnvf(GL_TEXTURE_ENV,GL_TEXTURE_ENV_MODE,GL_COMBINE_ARB);
glTexEnvf(GL_TEXTURE_ENV,GL_RGB_SCALE_ARB,1);
glTexEnvf(GL_TEXTURE_ENV,GL_COMBINE_RGB_ARB,GL_DOT3_RGB_ARB);
glTexEnvf(GL_TEXTURE_ENV,GL_SOURCE0_RGB_ARB,GL_PREVIOUS_ARB);
glTexEnvf(GL_TEXTURE_ENV,GL_SOURCE1_RGB_ARB,GL_TEXTURE);
glTexEnvf(GL_TEXTURE_ENV,GL_OPERAND0_RGB_ARB,GL_SRC_COLOR);
glTexEnvf(GL_TEXTURE_ENV,GL_OPERAND1_RGB_ARB,GL_SRC_COLOR);
// la troisième contient la texture d'atténuation
glActiveTextureARB(GL_TEXTURE2_ARB);
glEnable(GL_TEXTURE_3D_EXT);
glBindTexture(GL_TEXTURE_3D_EXT,lightmap );
glTexEnvf(GL_TEXTURE_ENV,GL_TEXTURE_ENV_MODE,GL_MODULATE);
// la quatrième contient la texture de diffuse
glActiveTextureARB(GL_TEXTURE3_ARB);
glEnable(GL_TEXTURE_2D);
glBindTexture(GL_TEXTURE_2D,textureId );
glTexEnvf(GL_TEXTURE_ENV,GL_TEXTURE_ENV_MODE,GL_MODULATE);
// on doit activer le blending additif pour pouvoir utiliser ce mode d'éclairage
glEnable(GL_BLEND);
glBlendFunc(GL_ONE,GL_ONE);
glDepthMask(GL_FALSE);
// on ajoute nos lumières
model->addLightCubeMap(light1);
model->addLightCubeMap(light2);
// on désactive la quatrième unité de texture
glActiveTextureARB(GL_TEXTURE3_ARB);
glDisable(GL_TEXTURE_2D);
// on désactive la troisième unité de texture
glActiveTextureARB(GL_TEXTURE2_ARB);
glDisable(GL_TEXTURE_3D_EXT);
// on désactive la seconde unité de texture
glActiveTextureARB(GL_TEXTURE1_ARB);
glDisable(GL_TEXTURE_2D);
// on désactive la première unité de texture
glActiveTextureARB(GL_TEXTURE0_ARB);
glDisable(GL_TEXTURE_CUBE_MAP_ARB);
// on désactive le blending
glDepthMask(GL_TRUE);
glDisable(GL_BLEND);Et maintenant, le code pour avoir des lumières colorées. Ce code s'ajoute simplement à la suite du précédent (mais avant la désactivation du blending).
glActiveTextureARB(GL_TEXTURE0_ARB);
glEnable(GL_TEXTURE_3D_EXT);
glBindTexture(GL_TEXTURE_3D_EXT,lightmap );
glTexEnvf(GL_TEXTURE_ENV,GL_TEXTURE_ENV_MODE,GL_MODULATE);
glBlendFunc(GL_DST_COLOR,GL_ONE);
model->renderColor(light1);
model->renderColor(light2);
glActiveTextureARB(GL_TEXTURE0_ARB);
glDisable(GL_TEXTURE_3D_EXT);Et voilà le résultat final de notre gestion de l'éclairage par pixel avec comme d'habitude trois lumières : une rouge, une bleue et une blanche.
IV. Conclusions▲
Ça y est, nous avons une gestion de l'éclairage par pixel fonctionnelle et complète. Enfin, complète, c'est très relatif. Comme je le disais au début de ce tutoriel, on en veut toujours plus, et, si vous vous souvenez du premier tutoriel, j'avais parlé de la composante spéculaire de la lumière, or, elle n'est pas gérée ici. C'est pourquoi nous allons voir dans le prochain tutoriel comment mettre en place un système de gestion des lumières complexes basé sur l'utilisation de shaders. Nous y verrons donc comment gérer la composante spéculaire de l'éclairage et en plus, nous y ajouterons la gestion du parallax mapping (aussi appelé offset bump mapping), qui permet de déformer les textures pour donner un effet de relief impressionnant pour un coût très faible.
Néanmoins, la technique présentée ici peut être très suffisante pour la plupart des moteurs graphiques amateurs. En effet, il ne faut pas oublier que si l'éclairage par pixel a un très bon rendu visuel, il impose au graphiste de créer des normal maps pour les modèles et pour le niveau, ce qui est un surcoût important en temps de production, et le modèle d'éclairage présenté dans le prochain tutoriel sera encore plus coûteux en termes de création de textures.
Il existe une technique permettant de se passer de cube map de normalisation, mais qui n'est pas non plus totalement satisfaisante. Elle consiste à stocker des vecteurs directement dans la texture 3D. Chaque vecteur pointe vers le centre de la texture, et surtout, sa longueur est proportionnelle à l'éloignement du texel par rapport au centre de la texture. On a donc des vecteurs dont la norme est proche de 1 vers le centre de la texture et nulle sur les bords de la texture. Ainsi, la texture 3D permet de stocker en même temps les vecteurs vers la lumière et l'atténuation de l'éclairage. Le problème de cette méthode est que les texels au centre de la texture vont eux aussi être nuls (car pointant sur eux-mêmes étant donné qu'ils sont au centre). On a donc un trou noir au centre de notre lumière. Si la lumière ne s'approche pas trop des polygones, cet artefact ne se verra pas, mais ça n'en reste pas moins une limitation importante. Je ne présenterai donc pas plus en détail cette technique.
Liens▲
Vous pouvez télécharger les sources de ce tutoriel ici ou ici [http]
Une version PDF de ce tutoriel est disponible ici ou ici [http]





