I. Les concepts liés à la lumière▲
Dans cette partie, je vais (re)présenter les concepts fondamentaux du fonctionnement de la lumière, puis je parlerai d'une notion très liée à la lumière : la gestion des materials, et finalement, je parlerai du parallax mapping.
I-A. L'éclairage spéculaire▲
Nous avons déjà vu dans les tutoriels précédents une grande partie du fonctionnement de la lumière. Nous savons donc comment calculer l'atténuation de la lumière via une texture 3D d'atténuation. Nous avons aussi vu comment prendre en compte l'orientation de la face par pixel grâce au calcul du produit scalaire via l'extension env_dot3. Il ne nous reste plus qu'à voir comment fonctionne la composante spéculaire de la lumière.
La composante spéculaire de la lumière est en fait la capacité qu'a une surface à refléter la lumière. On parle souvent de reflets spéculaires. Pour bien voir ce que représente cette composante spéculaire, il suffit d'imaginer la différence entre une surface chromée et un pneu. Les deux surfaces seront noires en l'absence de lumière, mais s'il y a une lumière, la surface chromée sera plus brillante que le pneu. Ceci est dû au fait que la surface chromée renvoie plus de lumière que le pneu qui, au contraire, en absorbe la majeure partie.
Pour calculer la composante spéculaire, il suffit de calculer le produit scalaire entre la normale à la surface et le vecteur de demi-angle… qu'est-ce que c'est que le vecteur de demi-angle ? C'est tout simplement le vecteur représentant la moitié de l'angle entre le vecteur vers la lumière et le vecteur vers la caméra. Comme ce vecteur dépend de la position de la caméra, nous avons donc bien un calcul qui va changer en fonction de la caméra et donc donner l'impression de reflet.
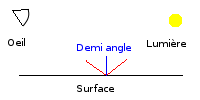
Pour calculer le vecteur de demi-angle, rien de plus simple, il suffit d'additionner le vecteur vers la lumière et le vecteur vers la caméra, et on obtient notre vecteur. Il ne nous reste plus qu'à le normaliser et voilà, on peut calculer notre produit scalaire pour obtenir la composante spéculaire. Malheureusement, si on effectue simplement le calcul comme cela, on obtient une surface bien trop réfléchissante. Pour réduire cet effet de surbrillance, on utilise une fonction puissance qui va réduire la réflexivité des pixels peu éclairés tout en préservant la luminosité des pixels fortement éclairés.
Voici le résultat de la composante spéculaire seule sans utiliser de fonction puissance :
Et le résultat avec fonction puissance :
On perçoit nettement mieux l'impression que la lumière se reflète sur les surfaces avec une fonction puissance. Dans ce tutoriel, le reflet spéculaire est mis à la puissance 8.
Le but de la composante spéculaire étant de faire saturer la couleur des pixels aux endroits de forte réflexion, elle est donc additionnée aux autres composantes de la lumière. Le calcul de la luminosité finale devient donc :
Luminosité = ambiante + ( (diffuse + spéculaire) * atténuation)
Le problème avec cette équation, c'est qu'elle impose d'avoir le même taux de reflets spéculaires sur toute la surface, or il est intéressant de pouvoir spécifier cela par pixel pour pouvoir, par exemple, simuler des surfaces brillantes par endroit et mates à d'autres endroits. Un bon exemple pour comprendre l'intérêt de pouvoir moduler la composante spéculaire est une plaque de métal rouillée. Là où le métal n'est pas rouillé, on a un reflet spéculaire maximum, mais là où il est rouillé, il n'y a pas de reflet. Pour mieux illustrer l'intérêt de la composante spéculaire, voici deux images de notre scène finale : la première sans reflet spéculaire.
Et le deuxième avec des reflets spéculaires.
Pour pouvoir effectuer cela, nous allons utiliser une gloss map, qui est une des composantes des materials que nous allons voir maintenant.
I-B. Les materials▲
Dans le model d'éclairage d'OpenGL, on peut spécifier à chaque vertex sa couleur ambiante, sa couleur diffuse, et sa couleur spéculaire, or maintenant, nous n'utilisons plus de l'éclairage par vertex, mais par pixel. Il est dommage de devoir spécifier ces composantes par vertex alors que le reste des calculs d'éclairage va se faire par pixel. C'est pour cela que nous avons besoin de la même notion de materials qu'OpenGL, mais cette fois-ci par pixel (pour pouvoir simuler l'effet de la plaque de métal rouillée vue plus haut par exemple.). Pour cela, nous allons utiliser plusieurs textures par material.
- La texture de diffuse : elle représente la couleur du material à son éclairage maximum. Contrairement aux textures qu'on aperçoit généralement dans les jeux, notre texture de diffuse ne doit par contenir d'information d'éclairage, c'est-à-dire, qu'elle ne doit pas être préombrée, sinon, ces informations d'éclairage vont entrer en conflit avec notre éclairage en temps réel (en étant mal orienté par exemple). Voici la texture de diffuse utilisée dans ce tutoriel.

- La normal map : bien qu'elle ne soit pas une des composantes directes de l'éclairage, la normal map nous sert à calculer la composante diffuse et spéculaire. Elle représente le volume virtuel de notre surface comme nous l'avons vu dans le quatrième tutoriel. Pour réduire la place occupée sur le disque par les textures, on peut retirer la normal map de la height map, que nous verrons plus loin, mais je ne le fais pas dans ce tutoriel. Voici la normal map utilisée dans ce tutoriel.

- La gloss map : Comme nous l'avons vu plus haut, la gloss map permet de spécifier par pixel l'intensité, mais aussi la couleur des reflets spéculaires. On peut par exemple faire une gloss map jaune pour l'utiliser sur un material représentant de l'or, ainsi, on s'assure que, quelle que soit la couleur de la lumière qui éclaire notre surface, le reflet spéculaire sera toujours jaune. Voici la gloss map utilisée dans ce tutoriel.

- La height map : ici, la height map n'entre pas dans le calcul de la lumière (bien qu'on puisse l'utiliser pour calculer la normal map), mais elle va nous servir au calcul du parallax mapping. La height map est une texture représentant, comme son nom l'indique, la hauteur de chaque pixel. Il peut être préférable d'utiliser des height maps servant à générer des normal maps au lieu d'utiliser directement des normal maps pour plusieurs raisons. En effet, une height map en niveau de gris prend moins de place sur le disque, permet de générer la normal map et de parallax mapping, mais il y a aussi des considérations qualitatives que je ne présenterai pas ici. Voici la height map utilisée dans ce tutoriel.

Vous aurez peut être remarqué qu'il n'y a pas d'ambiante map… Cela est dû au fait que la lumière ambiante peut être obtenue à partir de la texture de diffuse.
I-C. Le parallax mapping▲
Bien qu'il ne soit pas directement lié à la gestion de la lumière, le parallax mapping n'est néanmoins utilisable qu'avec un système d'éclairage par pixel. En effet, le parallax mapping consiste à déformer les textures en fonction d'une height map pour obtenir un effet de volume plus prononcé qu'avec simplement du bump mapping. Il n'y a donc aucun intérêt à utiliser du parallax mapping avec du simple light mapping par exemple.
Un gros avantage du parallax mapping est qu'il est très peu consommateur en ressources et qu'il est facile à mettre en œuvre. En effet, il suffit d'avoir une height map (on peut la stocker dans la composante alpha de la normal map) et un vecteur du pixel vers la caméra pour calculer les nouvelles coordonnées de textures déformées.
Le parallax mapping consiste simplement à calculer un décalage dans les coordonnées de textures en fonction de la direction du pixel par rapport à la caméra et de la hauteur du pixel dans la height map. Ceci se résume à trois lignes supplémentaires dans le fragment program. Encore une fois, pour bien voir la différence, rien ne vaut des images comparatives avec/sans.
On peut voir que les pierres ont été déformées pour donner une meilleure impression de volume, mais surtout, cette déformation se fait par rapport à la position de la caméra, donc si la caméra bouge, la déformation va se modifier pour prendre en compte la nouvelle direction de la caméra.
II. Modifications apportées au programme▲
Dans cette partie, nous allons voir les modifications apportées au programme. Nous verrons d'abord la nouvelle gestion des extensions mises en place pour ce tutoriel, puis nous verrons les modifications apportées au rendu des modèles. Je détaillerai ensuite les vertex et fragment program utilisés dans le tutoriel, puis, finalement, nous verrons comment mettre en place le rendu final de nos lumières.
II-A. Gestion des extensions▲
Depuis le deuxième tutoriel, nous avons ajouté à chaque nouveau tutoriel de nouvelles extensions. Bien que nous n'ayons pas chargé toutes les fonctions liées à ces extensions, notre fonction de chargement des extensions devient de plus en plus grosse. Il nous faut aussi passer les fonctions aux classes qui vont les utiliser (la classe de modèles utilise les fonctions du multitextuing par exemple), ce qui implique l'utilisation de nombreuses variables externes. Pour faciliter la gestion des extensions, nous utiliserons désormais GLEW. GLEW est une bibliothèque qui permet de gérer facilement et de façon totalement transparente les extensions OpenGL. En utilisant GLEW, notre fonction de chargement des extensions devient simplement ça :
void initExtensions()
{
GLenum err = glewInit();
if (GLEW_OK != err)
{
// impossible d'initialiser glew
fprintf(stderr, "Erreur à l'initialisation de GLEW : %s\n", glewGetErrorString(err));
exit(0);
}
if (!glewIsSupported("GL_ARB_multitexture"))
{
fprintf(stderr,"votre carte ne supporte pas l'extension GL_ARB_multitexture\n");
exit(0);
}
if (!glewIsSupported("GL_EXT_texture3D"))
{
fprintf(stderr,"votre carte ne supporte pas l'extension GL_ARB_multitexture\n");
exit(0);
}
if (!glewIsSupported("GL_ARB_texture_env_dot3"))
{
fprintf(stderr,"votre carte ne supporte pas l'extension GL_ARB_texture_env_dot3\n");
exit(0);
}
if (!glewIsSupported("GL_ARB_texture_cube_map"))
{
fprintf(stderr,"votre carte ne supporte pas l'extension GL_ARB_texture_cube_map\n");
exit(0);
}
if (!glewIsSupported("GL_ARB_vertex_program"))
{
fprintf(stderr,"votre carte ne supporte pas l'extension GL_ARB_vertex_program\n");
exit(0);
}
if (!glewIsSupported("GL_ARB_fragment_program"))
{
fprintf(stderr,"votre carte ne supporte pas l'extension GL_ARB_fragment_program\n");
exit(0);
}
}Ici, on vérifie simplement que la carte supporte bien les extensions, mais on ne les charge pas, c'est la fonction glewInit qui s'en est chargée pour nous. Nous pouvons maintenant utiliser toutes nos fonctions supportées par la carte comme si elles étaient des fonctions standard OpenGL.
Lors de l'inclusion du header glew.h, bien vérifier que l'inclusion est placée avant celle du fichier gl.h.
II-B. Modification du rendu des modèles▲
Ici, pas de gros changements. Nous allons juste modifier la méthode d'ajout d'une lumière. Comme nous allons utiliser un vertex program, l'ensemble des calculs effectués par vertex se feront dans le vertex program, ce qui va réduire d'autant notre fonction d'ajout des lumières. La seule chose à bien comprendre ici, c'est que nous devons envoyer certaines informations au vertex/fragment program comme les trois vecteurs de l'espace local du vertex ou encore la position de la lumière et son rayon. Pour cela, j'utilise les coordonnées de textures, mais on aura très bien pu passer par des tableaux d'attributs… À part cela, la méthode est assez simple à comprendre puisqu'il ne s'agit que d'envoyer la géométrie à la carte graphique, plus les informations nécessaires aux calculs. Le code de la méthode donne donc ça :
void Model::addLightCubeMap(Light& light)
{
Vecteur lightPos = light.getPosition();
// on passe la couleur de la lumière
glColor3f(light.getColor().r,light.getColor().g,light.getColor().b);
// on passe la position de la lumière et son rayon dans la coordonnée de texture 1
glMultiTexCoord4fARB(GL_TEXTURE1_ARB,lightPos.x,lightPos.y,lightPos.z,
1/light.getRadius());
glBegin(GL_TRIANGLES);
for(int i = 0;i < nbFaces; i++)
{
for (int j = 0; j < 3; j++)
{
int vertexIndex = faces[i].vertexIndex[j];
// on passe les tangentes, binormales et normales dans
// les coordonnées de textures 2,3 et 4
glMultiTexCoord3fARB(GL_TEXTURE2_ARB,tangents[vertexIndex].x,
tangents[vertexIndex].y,tangents[vertexIndex].z);
glMultiTexCoord3fARB(GL_TEXTURE3_ARB,binormals[vertexIndex].x,
binormals[vertexIndex].y,binormals[vertexIndex].z);
glMultiTexCoord3fARB(GL_TEXTURE4_ARB,normals[vertexIndex].x,
normals[vertexIndex].y,normals[vertexIndex].z);
// on passe les coordonnées de la scène dans la coordonnée de texture 0
TexCoord &tc = texCoords[faces[i].texCoordIndex[j]];
glMultiTexCoord2fARB(GL_TEXTURE0_ARB,tc.u,tc.v);
Vecteur &v = vertex[vertexIndex];
glVertex3f(v.x,v.y,v.z);
}
}
glEnd();
}Ici, je n'envoie pas le rayon de la lumière, mais l'inverse de son rayon. Cela permet de réduire les calculs, car pour calculer l'atténuation j'ai besoin de faire une division par le rayon, or il est plus rapide de multiplier par l'inverse du rayon que de faire cette division directement dans le vertex/fragment program.
Comme d'habitude, je suppose ici qu'OpenGL est bien configuré, c'est-à-dire que les vertex/fragment programs sont bien activés, le blending est en mode additif, et les unités de textures sont bien positionnées.
II-C. Les vertex et fragment programs▲
Dans cette partie, je vais présenter le vertex program et le fragment program utilisés dans le tutoriel pour calculer l'éclairage. J'ai préféré utiliser des programs assembleurs ARB au lieu de vertex/fragment shaders ARB, car ceux-ci sont supportés par moins de cartes, mais aussi, car les programs sont en assembleur, ce qui est plus compliqué à mettre en œuvre, mais permet de mieux se rendre compte de l'étendue des calculs effectués par la carte graphique.
Dans un premier temps, il nous faut envoyer nos programs à OpenGL pour les compiler et les faire valider par la carte graphique. C'est le travail effectué par la méthode initShaders suivante.
void initShaders()
{
glGenProgramsARB(1, &fragmentProgramId);
glBindProgramARB(GL_FRAGMENT_PROGRAM_ARB, fragmentProgramId);
glProgramStringARB(GL_FRAGMENT_PROGRAM_ARB, GL_PROGRAM_FORMAT_ASCII_ARB,
strlen((char*) fragmentProgram), fragmentProgram);
if(GL_INVALID_OPERATION == glGetError() )
{
//une erreur est détectée
//récupère les informations sur l'erreur survenue
const unsigned char* errorString;
GLint errorPos = 0;
errorString=glGetString(GL_PROGRAM_ERROR_STRING_ARB);
glGetIntegerv(GL_PROGRAM_ERROR_POSITION_ARB,&errorPos);
fprintf(stderr,"une erreur est survenue a la position : %d\n%s\n",
errorPos, errorString);
// on affiche le program jusqu'à l'erreur
for (int i = 0; i < errorPos; i++)
{
printf("%c", fragmentProgram[i]);
}
printf("\n");
}
// chargement du vertex program
glGenProgramsARB(1, &vertexProgramId);
glBindProgramARB(GL_VERTEX_PROGRAM_ARB, vertexProgramId);
glProgramStringARB(GL_VERTEX_PROGRAM_ARB, GL_PROGRAM_FORMAT_ASCII_ARB,
strlen((char*) vertexProgram), vertexProgram);
if(GL_INVALID_OPERATION == glGetError())
{
//une erreur est détectée
//récupère les informations sur l'erreur survenue
const unsigned char* errorString;
GLint errorPos = 0;
errorString=glGetString(GL_PROGRAM_ERROR_STRING_ARB);
glGetIntegerv(GL_PROGRAM_ERROR_POSITION_ARB,&errorPos);
fprintf(stderr,"une erreur est survenue à la position : %d\n%s\n",
errorPos, errorString);
// on affiche le program jusqu'à l'erreur
for (int i = 0; i < errorPos; i++)
{
printf("%c", vertexProgram[i]);
}
printf("\n");
}
}Maintenant que nous avons chargé nos programs, nous allons voir ce qu'ils contiennent. Les explications des programs sont contenues directement en tant que commentaires pour éviter d'avoir à les découper en petites parties. D'abord, voilà le vertex program utilisé. Il effectue tous les calculs par vertex que nous faisions avant sur le CPU.
# vertex program utilisé pour gérer l'éclairage
# il effectue la projection du vecteur vers la lumière et
# du vecteur vers la caméra qui sont utilisés dans le fragment
# program par la suite.
# @param vertex.texcoord[0] : coordonnées de texture du polygone
# @param vertex.texcoord[1] : position de la lumière + rayon dans w
# @param vertex.texcoord[2] : tangente
# @param vertex.texcoord[3] : binormal
# @param vertex.texcoord[4] : normale
# @param vertex.texcoord[5] : position de la caméra
# @param vertex.color : couleur de la lumière
#
# @out result.texcoord[0] : coordonnée de texture du polygone
# @out result.texcoord[1] : vecteur du vertex vers la caméra
# @out result.texcoord[2] : vecteur du vertex vers la lumière
!!ARBvp1.0 OPTION ARB_position_invariant;
# mvit repesente l'inverse transposé de la matrice
# de modelview
PARAM mvit[4] = {state.matrix.modelview.invtrans};
# modelview est la matrice de modelview
PARAM modelView[4] = { state.matrix.modelview };
# camPos est la position de la caméra
# note : pour récupérer la position de la caméra,
# il suffit de prendre la quatrième ligne de l'inverse
# transposé de la matrice de modelview
PARAM camPos = state.matrix.modelview.invtrans.row[3];
# les texcoord 2 contiennent la tangente
ATTRIB tangent = vertex.texcoord[2];
# les texcoord 3 contiennent la binormale
ATTRIB binormal = vertex.texcoord[3];
# les texcoord 4 contiennent la normale
ATTRIB normal = vertex.texcoord[4];
# les texcoord 1 contiennent les informations sur
# la lumière, c.-à-d. : sa position et l'inverse de
# son rayon dans la composante w
ATTRIB lightInfo = vertex.texcoord[1];
TEMP vertexToLight;
TEMP vertexToCam;
TEMP temp;
# on projette le vecteur vers la lumière dans l'espace local
# du vertex
SUB temp, lightInfo, vertex.position ;
DP3 vertexToLight.x, temp, tangent;
DP3 vertexToLight.y, temp, binormal;
DP3 vertexToLight.z, temp, normal;
MOV vertexToLight.w, lightInfo.w;
# on projette le vecteur vers la caméra dans l'espace local
# du vertex
SUB temp, camPos, vertex.position;
DP3 vertexToCam.x, temp, tangent;
DP3 vertexToCam.y, temp, binormal;
DP3 vertexToCam.z, temp, normal;
# ici, je ne normalise pas les vecteurs calculés, ce sera
# fait dans le fragment program pour améliorer la qualité
# de l'affichage (plus de problèmes de normalisation dus à
# l'interpolation)
# on copie les informations calculées sur les sorties du
# vertex program.
MOV result.texcoord[0], vertex.texcoord[0];
MOV result.texcoord[1], vertexToCam;
MOV result.texcoord[2], vertexToLight;
MOV result.color, vertex.color;
ENDEt maintenant, voilà le fragment program qui calcule le résultat final de notre ajout de lumière.
# fragment program gérant l'affichage de la lumière
# ce fragment program calcule l'éclairage avec reflets
# spéculaires et avec du parallax mapping.
# @param texture[0] : normal map
# @param texture[1] : diffuse map
# @param texture[2] : height map
# @param texture[3] : gloss map
# @param texture[4] : atténuation map
# @param fragment.texcoord[0] : coordonnées de texture du polygone
# @param fragment.texcoord[1] : vecteur du fragment vers la caméra
# @param fragment.texcoord[2] : vecteur de fragment vers la lumière
# @param fragment.color : la couleur de la lumière
!!ARBfp1.0 OPTION ARB_precision_hint_fastest;
PARAM power = {8,0,0,0};
# la texture de normal map
TEMP normal;
# la texture d'atténuation
TEMP attenuation;
# la texture de diffuse
TEMP diffuse;
# la texture de gloss
TEMP gloss;
# la texture de height map
TEMP height;
# les coordonnées de textures modifiées par
# le parallax mapping
TEMP newTexcoord;
# le vecteur allant du fragment vers la lumière
TEMP toLight;
# la couleur finale du fragment
TEMP final;
# le résultat du produit scalaire entre la normale
# et le vecteur vers la lumière
TEMP NdotL;
# vecteur temporaire
TEMP temp;
# le vecteur de demi-angle pour la spéculaire
TEMP halfAngle;
# le vecteur du fragment vers la caméra
TEMP tocamera;
# la composante spéculaire de la lumière
TEMP specular;
# on normalise le vecteur fragment->lumière
# note : en l'absence d'extension permettant d'effectuer
# la normalisation d'un vecteur en une instruction, il faut
# utiliser la séquence suivante pour normaliser un vecteur
# (ici on normalise fragment.texcoord[2])
DP3 temp, fragment.texcoord[2], fragment.texcoord[2];
RSQ temp, temp.x;
MUL toLight, fragment.texcoord[2], temp;
# on normalise le vecteur fragment->caméra
DP3 temp, fragment.texcoord[1], fragment.texcoord[1];
RSQ temp, temp.x;
MUL tocamera, fragment.texcoord[1], temp;
# on calcule les nouvelles coordonnées de textures pour le parallax mapping
TEX height, fragment.texcoord[0], texture[2], 2D;
MAD height, height, 0.04, -0.02;
MAD newTexcoord, height, tocamera, fragment.texcoord[0];
# on calcule l'atténuation
# on a texcoord[2] qui contient le vecteur vertex->lumière
# on divise le vecteur par le rayon de la lumière (w contient l'inverse du rayon)
# et on ajoute 0.5 pour partir du centre de la texture
# cf : calcul d'attenuation dans les tutoriels sur le light mapping.
MAD attenuation, fragment.texcoord[2], fragment.texcoord[2].w, {0.5,0.5,0.5,0};
TEX attenuation, atténuation, texture[4], 3D;
# on charge la normal map
TEX normal, newTexcoord, texture[0], 2D;
# on remap la normal dans [0..1] au lieu de [0.5..1]
MAD normal, normal, 2, -1;
# on renormalise la normal pour maximiser la qualité
# d'affichage (plus d'interpolation, tous les vecteurs
# sont bien normalisé)
DP3 temp, normal, normal;
RSQ temp, temp.x;
MUL normal, normal, temp;
# on effectue le produit scalaire entre la
# normale à la surface et le vecteur transformé
# vers la lumière.
DP3 NdotL, normal, toLight;
MAX NdotL, NdotL, 0;
MUL_SAT final, NdotL, fragment.color;
# calcul de la composante spéculaire
# on calcule le vecteur de demi-angle normalisé
ADD halfAngle, tocamera, toLight;
DP3 temp, halfAngle, halfAngle;
RSQ temp, temp.x;
MUL halfAngle, halfAngle, temp;
# on effectue le calcul du produit scalaire entre la
# normale à la surface et le vecteur de demi-angle.
# on s'assure que la composante spéculaire n'est pas
# inférieure à 0, ce qui entrainerait des problèmes lors
# de l'addition avec le reste du calcul. En effet, la
# composante spéculaire peut ajouter de la luminosité à un
# fragment, mais ne doit pas en retirer.
DP3 specular, normal, halfAngle;
MAX specular, specular, 0;
# on met le résultat à la puissance en paramètre
POW specular, specular.x, power.x;
# on multiplie par la couleur de la lumière
MUL specular, specular, fragment.color;
# on récupère les textures restantes
TEX diffuse, newTexcoord, texture[1], 2D;
TEX gloss, newTexcoord, texture[3], 2D;
# on termine l'équation d'éclairage
# on multiplie la composante spéculaire par le gloss
MUL specular, specular, gloss;
# on multiplie le bump par la texture de diffuse et
# on ajoute la composante spéculaire
MAD final, final, diffuse, specular;
# on atténue le tout
MUL final, final, atténuation;
# et on envoie le résultat du calcul en tant que couleur
# finale.
MOV result.color, final;
ENDSi vous n'êtes pas familier avec les vertex/fragment programs ARB, ceux-ci peuvent vous sembler incompréhensibles, et pourtant ils ne font que des calculs assez simples à comprendre. Si vraiment vous ne comprenez pas, vous pouvez toujours aller regarder une doc sur les instructions des programs ARB.
Il faut bien se rendre compte que l'ensemble des calculs du fragment program sont effectués pour chaque pixel, même si le pixel est finalement noir. On obtient donc un fragment program relativement coûteux en termes de fill rate (1). On peut réduire ce coût en ne renormalisant pas la normal map et en effectuant les calculs de normalisation des vecteurs vers la lumière et la caméra au niveau du vertex program, mais c'est aux dépens de la qualité, et on retombe sur les problèmes d'interpolation si on n’utilise pas de cube map de normalisation comme c'est le cas ici.
II-D. Le rendu final▲
Maintenant que nous avons toutes les informations nécessaires, nous pouvons voir comment effectuer le rendu final de la scène. Le code nécessaire est assez semblable à celui du tutoriel précédent, mis à part qu'on n'a plus à activer l'extension env_dot3 pour l'unité de texture de la normal map, qu'on doit activer par contre les vertex/fragment programs et qu'on n'a pas à effectuer de deuxième passe pour avoir des lumières colorées. On ajoute aussi l'utilisation de la height map et de la gloss map, ce qui fait que nous utilisons maintenant cinq unités de textures pour notre rendu (et nous n'utilisons plus de cube map de normalisation). Le code de rendu de la scène donne donc :
// on configure la première unité de texture :
// elle contient la texture de la scène
glActiveTextureARB(GL_TEXTURE0_ARB);
glEnable(GL_TEXTURE_2D);
glBindTexture(GL_TEXTURE_2D, textureId);
glTexEnvf(GL_TEXTURE_ENV,GL_TEXTURE_ENV_MODE,GL_MODULATE);
// on effectue le rendu de la lumière ambiante
model->initLighting(ambiant);
// on doit reconfigurer les unités de textures
// la première unité de texture contient la normal map
glActiveTextureARB(GL_TEXTURE0_ARB);
glEnable(GL_TEXTURE_2D);
glBindTexture(GL_TEXTURE_2D, normalMapId);
// la deuxième contient la texture de diffuse
glActiveTextureARB(GL_TEXTURE1_ARB);
glEnable(GL_TEXTURE_2D);
glBindTexture(GL_TEXTURE_2D,textureId );
// la troisième contient la height map
glActiveTextureARB(GL_TEXTURE2_ARB);
glEnable(GL_TEXTURE_2D);
glBindTexture(GL_TEXTURE_2D,heightMapId );
// la quatrième contient la gloss map
glActiveTextureARB(GL_TEXTURE3_ARB);
glEnable(GL_TEXTURE_2D);
glBindTexture(GL_TEXTURE_2D,glossMapId );
// la cinquième contient la texture d'atténuation
glActiveTextureARB(GL_TEXTURE4_ARB);
glEnable(GL_TEXTURE_3D_EXT);
glBindTexture(GL_TEXTURE_3D_EXT,lightmap );
// on doit activer le blending additif pour pouvoir utiliser
// ce mode d'éclairage
glEnable(GL_BLEND);
glBlendFunc(GL_ONE,GL_ONE);
glDepthMask(GL_FALSE);
// on active les vertex/fragment program
glEnable(GL_VERTEX_PROGRAM_ARB);
glBindProgramARB(GL_VERTEX_PROGRAM_ARB,vertexProgramId);
glEnable(GL_FRAGMENT_PROGRAM_ARB);
glBindProgramARB(GL_FRAGMENT_PROGRAM_ARB,fragmentProgramId);
// on ajoute nos lumières
model->addLightCubeMap(light1);
model->addLightCubeMap(light2);
// on désactive les vertex/fragment program
glDisable(GL_VERTEX_PROGRAM_ARB);
glDisable(GL_FRAGMENT_PROGRAM_ARB);
// on désactive la cinquième unité de texture
glActiveTextureARB(GL_TEXTURE4_ARB);
glDisable(GL_TEXTURE_3D_EXT);
// on désactive la quatrième unité de texture
glActiveTextureARB(GL_TEXTURE3_ARB);
glDisable(GL_TEXTURE_2D);
// on désactive la troisième unité de texture
glActiveTextureARB(GL_TEXTURE2_ARB);
glDisable(GL_TEXTURE_2D);
// on désactive la seconde unité de texture
glActiveTextureARB(GL_TEXTURE1_ARB);
glDisable(GL_TEXTURE_2D);
// on désactive la première unité de texture
glActiveTextureARB(GL_TEXTURE0_ARB);
glDisable(GL_TEXTURE_CUBE_MAP_ARB);
glDepthMask(GL_TRUE);
glDisable(GL_BLEND);Et voilà le résultat final en image.
III. Réflexions sur la gestion de la lumière▲
Nous avons vu au cours de cette série de tutoriels comment gérer la lumière de plusieurs façons différentes. Cela va de la plus simple, avec l'éclairage par vertex, à des plus compliquées comme nous venons de le voir. Comme je le disais dans la conclusion du tutoriel précédent, l'utilisation d'une méthode d'éclairage ou d'une autre influe non seulement sur les performances du moteur 3D, mais aussi sur la quantité de ressources à fournir pour les artistes. En effet, avec un système complexe, le créateur de textures aura à créer :
- une texture de diffuse standard. Elle correspond à la texture généralement créée pour un système d'éclairage simple. Ce n'est donc pas un surcoût ici ;
- une height map utilisée pour gérer l'effet de parallax mapping ;
- une normal map. Bien que généralement créée à partir de la height map, on peut parfois souhaiter avoir une normal map différente. C'est sans doute la texture la plus importante d'un material. Une normal map de mauvaise qualité, et l'ensemble du système de gestion de la lumière en subit les conséquences ;
- une gloss map qui permet de nuancer l'effet de l'éclairage spéculaire. C'est une des textures les plus difficiles à régler. Une gloss map qui atténue trop l'éclairage spéculaire, l'effet perd de son intérêt, au contraire, si la gloss map ne l'atténue pas assez, on se retrouve avec des surfaces qui ressemblent à du plastique ou du métal trop brillant ;
- une texture émissive. Bien que je ne l'aie pas traitée dans ce tutoriel, on peut souhaiter avoir certaines parties de notre texture toujours éclairées. Par exemple un bouton lumineux ou un écran d'ordinateur émettent leur propre lumière. Pour cela on utilise une texture émissive qui est affichée durant la première passe de l'algorithme de rendu de la lumière (le rendu de la lumière ambiante).
Nous avons donc ici de nombreuses textures à créer pour nos artistes, ce qui peut considérablement alourdir le processus de création d'un jeu vidéo pour une équipe d'amateurs.
Un autre point important que je n'est pas traité ici est l'optimisation du rendu des lumières. Nos lumières étant des lumières sphériques ponctuelles, on peut effectuer de nombreuses optimisations avant de les afficher. En dehors des algorithmes de partitionnement (BSP, octree, portals), la première optimisation qui vient à l'esprit est de vérifier si la face est bien orientée vers la lumière avant de la rendre. En effet, il est inutile de dessiner une face si on sait que l'ensemble de ses vertex tournent le dos à la lumière. Si ceci peut être coûteux pour l'éclairage par vertex (le coût de vérification par face sera supérieur au gain de vitesse), cette optimisation peut être très intéressante pour les systèmes plus coûteux en termes de fill rate, c'est-à-dire, quand le dessin d'un pixel est lent (ce qui est notre cas dans ce tutoriel). On peut aussi exclure de l'affichage toutes les faces qui sont trop éloignées de la lumière pour être éclairées (ceci se fait simplement à l'aide d'une équation de plan par polygone).
Une autre optimisation simple à mettre en œuvre consiste à utiliser un rectangle de clipping autour de la lumière. Cette optimisation n'est utilisable que pour les rendus de lumière en multipasse, elle n'est donc pas applicable à l'éclairage par vertex. Elle consiste tout simplement à utiliser la possibilité des cartes graphiques à utiliser un rectangle de clipping pour réduire la zone de dessin autorisée. Si, en calculant les extremums de notre lumière, on en déduit un rectangle de clipping qui englobe entièrement notre lumière, on peut ainsi réduire l'affichage des grands polygones touchés par la lumière, et ainsi sauvegarder du fill rate encore une fois.
Un avantage de cette optimisation est qu'elle est aussi très utile pour optimiser le rendu des ombres utilisant l'algorithme des shadow volumes.
Comme je l'ai dit dans le premier tutoriel, je n'ai traité que des lumières sphériques ponctuelles directes. On peut imaginer des systèmes d'éclairage plus complexes gérant les spots de lumières via des projections de textures, et des lumières directionnelles infinies. De même, on peut espérer voir arriver dans l'industrie d'ici quelque temps l'utilisation de l'illumination globale qui permet de gérer les sources de lumière indirectes. Ceci est encore à l'heure actuelle un sujet de recherche important, mais les premiers résultats sont déjà impressionnants.
Un autre point important qui n'est pas traité dans cette série est la gestion de l'occlusion de la lumière, via des algorithmes de génération d'ombres portées. En effet, dans ces tutoriels, la lumière traverse les objets pour aller éclairer les autres objets. Ceci est embêtant pour le réalisme de notre scène. Il peut donc être intéressant d'avoir des ombres portées sur les autres objets, et pour cela utiliser des techniques comme les shadow volumes ou les shadow buffers (aussi appelée shadow maps).
IV. Conclusions▲
Ça y est, c'est fini. Si nous avons vu au cours de cette série de tutoriels comment gérer la lumière de plusieurs manières, il ne faut pas oublier que le principal argument pour le faire dans un moteur 3D amateur est bien de pouvoir dépasser la limite du nombre maximum de lumières hardware supportées par les cartes graphiques. Il est donc conseillé de choisir la méthode la plus adaptée au moteur que vous souhaitez réaliser. Il n'est pas forcement utile de mettre en place un système d'éclairage par pixel pour un moteur simple ou pour un jeu de stratégie par exemple, alors qu'une bonne gestion de l'éclairage pourra être très importante dans un FPS. Le principal est que maintenant vous avez le choix de la technique à utiliser dans votre moteur.
V. Liens▲
Vous pouvez télécharger les sources de ce tutoriel ici [http]










